
Theoretic basis for SyntheticOH
Excited OH-molecules in the upper mesosphere are created from the reactions:
Airglow spectra are created when molecules excited into higher vibrational and rotational states go to lower molecular states. The spectra consist of vibrational bands, which again are made up of rotational lines. In this program the spectrum of the hydroxyl radical is evaluated.
In order to derive the rotational temperatures, it is necessary to produce synthetic spectra. For this purpose knowledge about line strength and line wavelength is needed. While the wavelength is only dependent on the energy of a state-to-state transition, the line intensity is somewhat more complicated to infer. As this is dependent on both the transition probability and the number of molecules in the initial state. Below this is excavated further.
The energy loss of a transition between an upper and a lower molecular state determine the emission wavelength of a diatomic molecule. The upper and lower states can differ in vibrational, rotational and translational states. OH* in the upper mesosphere is in its translational ground state X2P making the wavelength of an emission (Herzberg 1950)
![]()
where G(v) is defined as the vibrational term in vibrational state v and F(J,v) is the rotational term in rotational state J and vibrational state v.
The vibrational term is
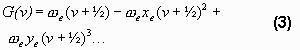
The vibrational constants (the Greek letter-coefficients in the formula) are taken from Krassovsky (1962). From the difference between G(6) and G(2) the main wavelength of the band can be found.
The rotational terms are
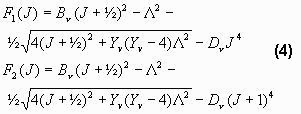
Here B, D and Y are functions of the vibrational state that are taken from (Krassovsky 1962). As it may be noticed, there are two rotational terms. This is due to the fact that the electron spin can be either up or down.
NOTE: Another splitting of these lines occur due to the so- called l-type doubling. This is an effect of the rotation of the nuclei (Krassovsky 1962). But this doubling is of no importance at normal instrument resolution, so it is not included in SyntheticOH.
Another important thing is that not all rotational transitions are possible. From the selection rule it is known that they only occur when DJ is –1, 0 or 1 giving rise to the P-, Q- and R-branch of the vibrational band (Herzberg 1950)
![]()
The intensity of a line in photon·s-1 is a product of the number of molecules in the upper state and the transition probability to end up in the lower state. Here the prime (´) is a symbol for the upper state and the double prime (´´) is a symbol for the lower state.
The transition probabilities are also called Einstein coefficients. The Einstein coefficients used in SyntheticOH are taken from Turnbull and Lowe (1989), Mies (1974) or Langhoff et al. (1986). The distribution of rotational levels in a certain vibrational state is defined by the Boltzmann distribution, if the molecules are in thermodynamical equilibrium. Thus making the number of molecules in the upper state
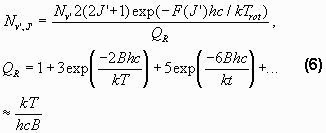
Trot is the rotational temperature, QR is the partition function and B is a constant. If the assumption of thermodynamical equilibrium is fulfilled Trot must be equal to the temperature of the surroundings. As this is the parameter of interest here, the goal of these theoretical speculations has now been reached. The only problem that remains is that Nv’ and Trot are both unknowns. Therefore it is only possible to calculate the relative strengths of the lines, making it necessary to have at least two lines in a vibrational-rotational band to obtain a temperature.
Pendleton et al. (1989) questioned whether OH* is in thermal equilibrium. They made spectral measurements of the (7,4)-band and came to the conclusion that for rotational levels above J´ = 5 this is not the case. In general whether OH* is in thermal equilibrium or not is definitely a question of vibrational and rotational level. As the lifetime of the molecule decreases when the vibrational or rotational level increases. The collision frequency in this altitude of the atmosphere is of the order 104s-1, while the average lifetime of OH in vibrational state 6 is of the order 10-2-10-3s (Turnbull and Lowe 1989).
Thus it would seem that, the lower vibrational state the better for deriving the temperature. This is not the case, as other factors have to be taken into consideration. The band should be in a wavelength region where clouds do not stop it and contamination from auroral bands should be avoided as far as possible.
The temperature is in practice derived by first finding the background level as a function of wavelength. To achieve this, synthetic spectra are calculated as a function of instrumental bandpass. The background is detected by choosing the optimal fit between the measured and the synthetic spectrum through iteration, to minimize the least square error. Secondly, when the background level is found, the temperature is derived from the slope of the linear fit to a Boltzmann plot (Log-energy term plot) using the measured P1 line intensities together with the equations described above (equations [5] and [6]). If the intensities of the associated P2 lines do not follow the same linear fit, then local thermal equilibrium has broken down, (cf. Pendleton et al., 1993), and the observation should be discarded. A more detailed description of the above temperature retrieval can be found in the work by Sivjee and Hamwey (1987).
References
Baker, D. J and A. T. Stair, Jr., Rocket Measurements of the Altitude Distributions of the Hydroxyl Airglow, Physica Scripta. Vol. 37, 611-622, 1988.
Herzberg, G., Spectra of Diatomic Molecules, D. Van Nostrad co., inc. New York, 1950.
Krassovsky, V. I., N. N. Shefov and V. I. Yarin, Atlas of the Airglow Spectrum 3000-12,400 Å, Planet. Space Sci. 1962.
Langhoff, S.R., Werner, H.J., and Rosmus, P., Theorical transitionsprobabilities for the OH Meinel system, Journal of Molecular Spectroscopy, 188(2), 507–529, 1986.
Mies, F. H., Calculated vibrational transition probabilities of OH(X 2 P), J. molec. Spectrosc., Vol. 118, 507, 1974.
Pendleton, W, P. Espy, D. Baker, A. Steed, M. Fetrow and K. Henriksen, Observation of OH Meinel (7,4) P(N´´ = 13) Transitions in the Night Airglow, Jour. of Geophys. Res. Vol. 94, No. A1, 505-510, 1989.
Pendleton, W.R., Jr., P.J. Espy, and M.R. Hammond, Evidence
for Non-Local-Thermodynamic-Equilibrium Rotation in the OH Nightglow,
J. Geophys. Res., 98, 11.567 - 11.579, 1993.
Sivjee, G. G. and R. M. Hamwey, Temperature and Chemistry of the Polar Mesopause OH, Jour. of Geophys. Res. Vol. 92, No. A5, 4663-4672, 1987.
Turnbull, D. N. and R. P. Lowe, New Hydroxyl Transition Probabilities and their Importance in Airglow Studies, Planet. Space Sci., Vol. 37, No. 6, 723-738, 1989.